- 2020-12-9
- ブログ
地名の研究 Ortsnamenanalyse (3)からの続きです
前回に掲載した「上位3PLZ」への集中度を補正する必要性について書きます。

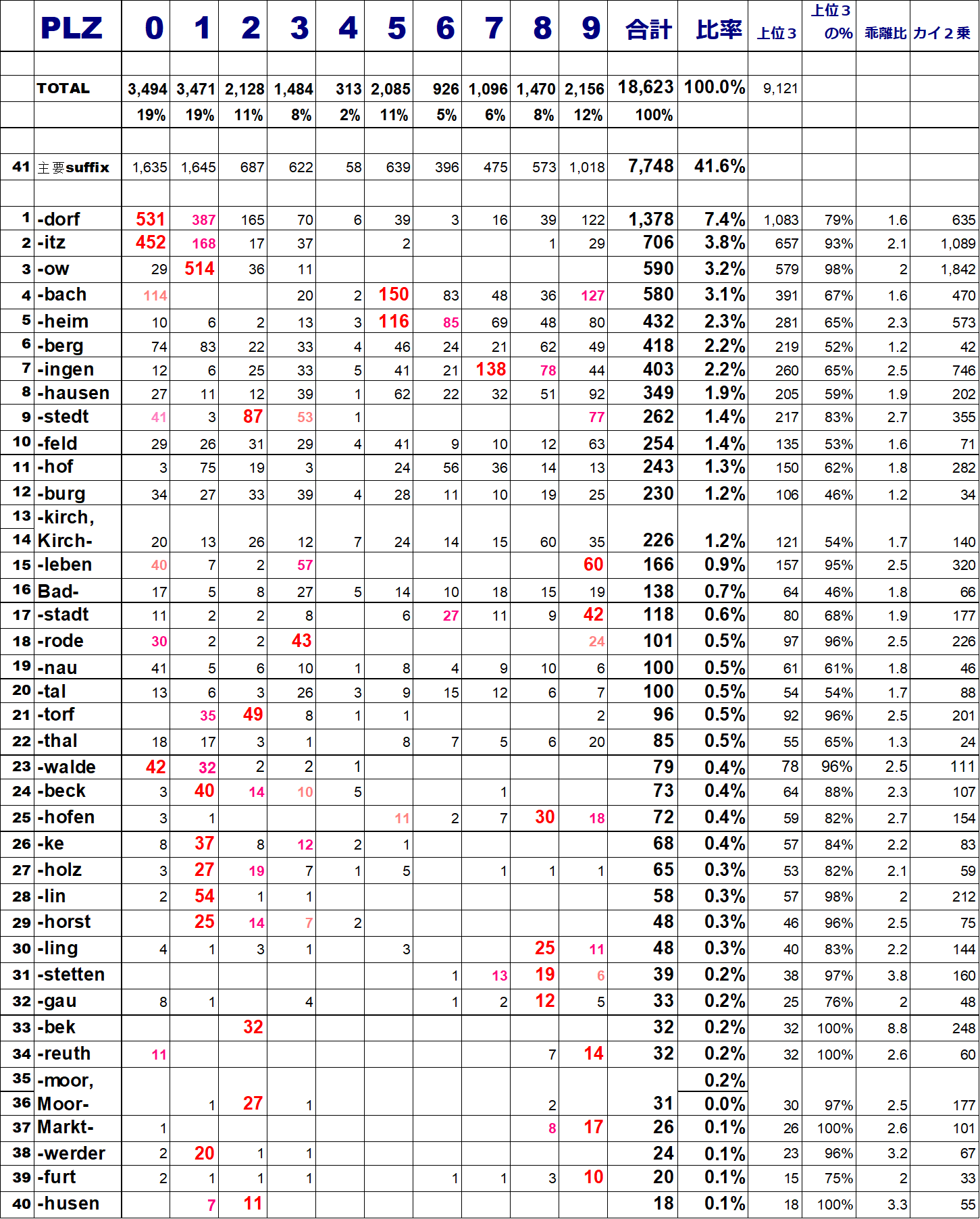
PLZに登録された地名 18,623件は、0~9までの PLZに上の表の赤で囲んだ部分にあるような比率で分布しています。前に書いたように、0と 1、すなわち旧東独東部に登録地名が多いく、逆に 4にはたった 313件しかない(0、1の 1/10以下)ことが分かります。
さて -dorfが付く地名が全ドイツに均等に分布していると仮定すると、この PLZの登録地名数の比率と同じ割合で配分されることが期待されます。ところが実態は青線で囲ったような分布をしています。ここで上位3PLZ(0、1、2)には -dorfの 79%が集中しています。仮定のように均等に分布していたとすると、それは 49%だったはず・・・そこでこの 79%を 49%で割ると 1.6となり、これは「均等に分布しているという仮定からどのくらい『乖離』しているか?」という指標になります。
この 1.6という数字自体には意味はありません。理想的に均等に分布しているとその数値は 1.0となるのは自明ですが、1.6がどのくらい偏っているのかを絶対値として定量化しているものではありません。しかし、例えば「上位3PLZへの集中度が同程度の2つの地名suffixの乖離値」を比較すると、それが大きい方がより偏った分布をしているということにはなるでしょう。
時節柄、ちょっと不謹慎な例えとはなりますが・・・地名の数という観点では「数の多い PLZ 0や 1は東京都や大阪府状態、数の少ない PLZ 4や 6は香川県のような状態」と言えるかもしれません。コロナ感染者が同じ 500人でも、そもそも人口が多い東京都や大阪府で起こったことと、鳥取県や香川県で起こったことでは、その「異常事態度合いが違う」・・・そんな相対指標と考えることもできるかもしれません。全体リストを再掲しておきますので、そういう視点で「乖離比」を見てみて下さい。
私のブログの読者はインクジェット業界の技術屋さんが多いことを想定して、超マニアックな余談ですが(笑)・・・この乖離比は「比」なので単位はありません。所謂「無次元数」です。そもそも、その前に「上位3PLZに集中しているパーセンテージ」や「均等に分布しているというパーセンテージ」自体が比率なので次元を持ちません。無次元数を無次元数で割った数値ですから当然「無次元」となります。そう、アイツです!有名な「無次元数特許」を思いつきますよね、インクジェット業界の技術屋さんなら?これ、特許申請しておこうかなあ(笑)
次回は本命の指標としての「カイ二乗分布」について書きます。こちらはマトモな話です(笑)
地名の研究 Ortsnamenanalyse (5)に続きます