- 2020-12-10
- ブログ
地名の研究 Ortsnamenanalyse (4)からの続きです
今回は本命の指標としての「カイ二乗分布」について書きます。面倒ならこの章はスキップしてもらってもいいですが、分かったら結構目からウロコですよ(笑)
統計を学んだ方や理系の方には既にお馴染みの話題かもしれませんが、Googleで「カイ二乗検定」を検索して改めて思ったのは、簡単な纏めなどと書きながら、結構難しい解説をしているなということでした。統計学の基礎知識があることを前提としていることが多いようです。そこで、ここでは多少の不正確さを承知の上で、敢えて文系の人にも分かり易い解説を試みます。
カイ二乗検定は「ある仮説から実態がどのくらいかけ離れているか?仮説は正しいのか?それとも無理筋なのか?」をチェックする手法です。ここでの目的は -dorf、-bergなどの「地名suffixが、PLZに関係なく、すなわち地域性や歴史的な経緯に関係なく、全ドイツに均等に分布している」と言えるかどうかを定量的・統計的に検定・確認するということになります。
カイ二乗は「ギリシャ文字χ(カイ)」の二乗という意味で、その値は下記の数式で示されます。
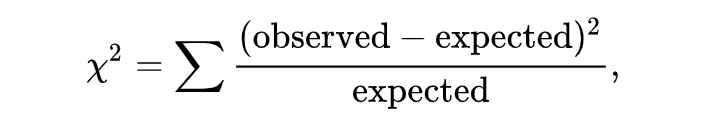
もうこの時点で逃げ出す人もいそうですが(笑)まあもう少しお付き合いください。日本語で書くとこうなります。

まずあまり深く考えずに計算してみましょう。もしある地名suffixが、PLZに関係なく、すなわち地域性や歴史的な経緯に関係なく、全ドイツに均等に分布しているとすれば、全地名のと同じ比率で各PLZに存在することが期待されます。これが理論値(期待値)です。ところが実際の観測値は、それとは別の分布をしています。これが観測値です。
これをエクセルの上で愚直に計算させてカイ二乗値を求めてみると、-dorfの事例では「635」となります。下のエクセルで確認してください。
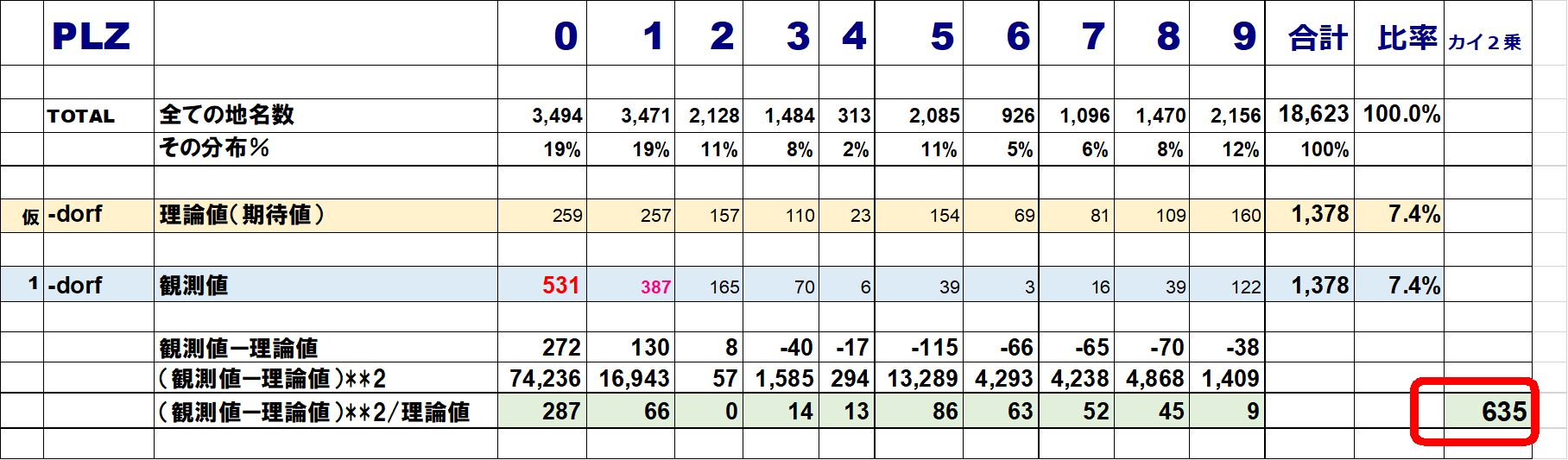
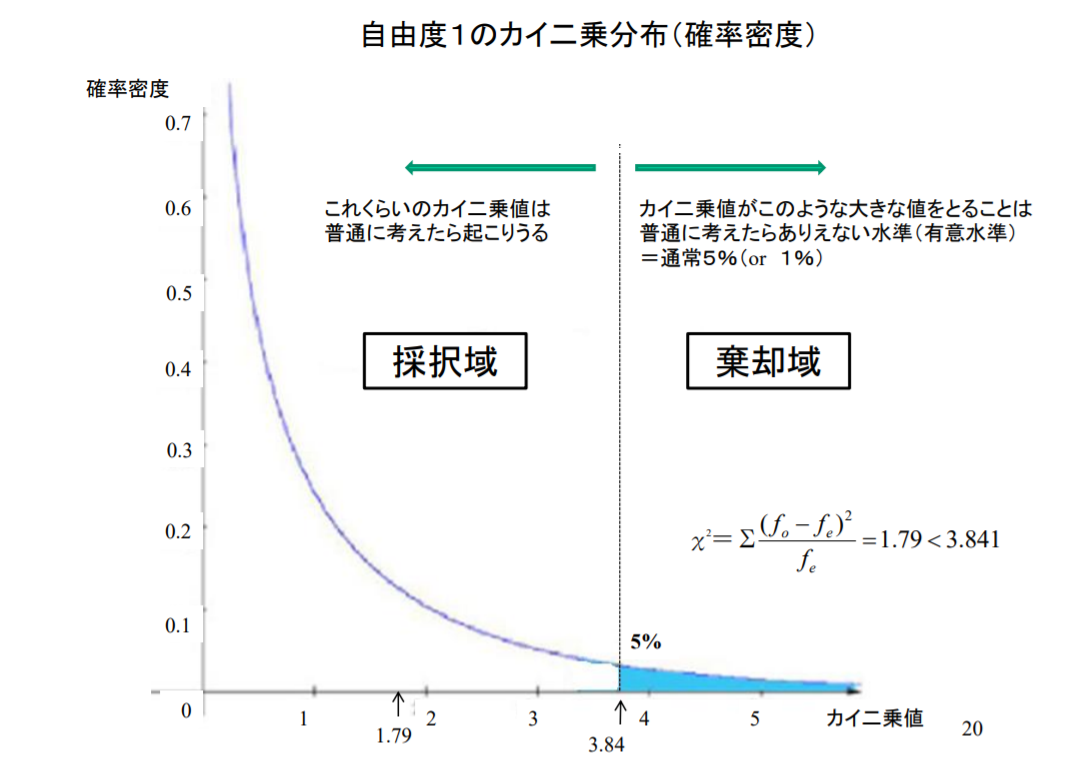
さて、この「635」って何なのさ?ということですが、それは右のグラフを見てください。この数字がかなり小さいと「仮説は採択される」=「ある地名suffixが、PLZに関係なく、すなわち地域性や歴史的な経緯に関係なく、全ドイツに均等に分布している」と言えるということです。
逆にある閾値を超えて大きな値だと「仮説は棄却される」=「ある地名suffixが、PLZに関係なく、すなわち地域性や歴史的な経緯に関係なく、全ドイツに均等に分布している」と言えないということになります。
この閾値を示しているのが下の「カイ二乗分布表」です
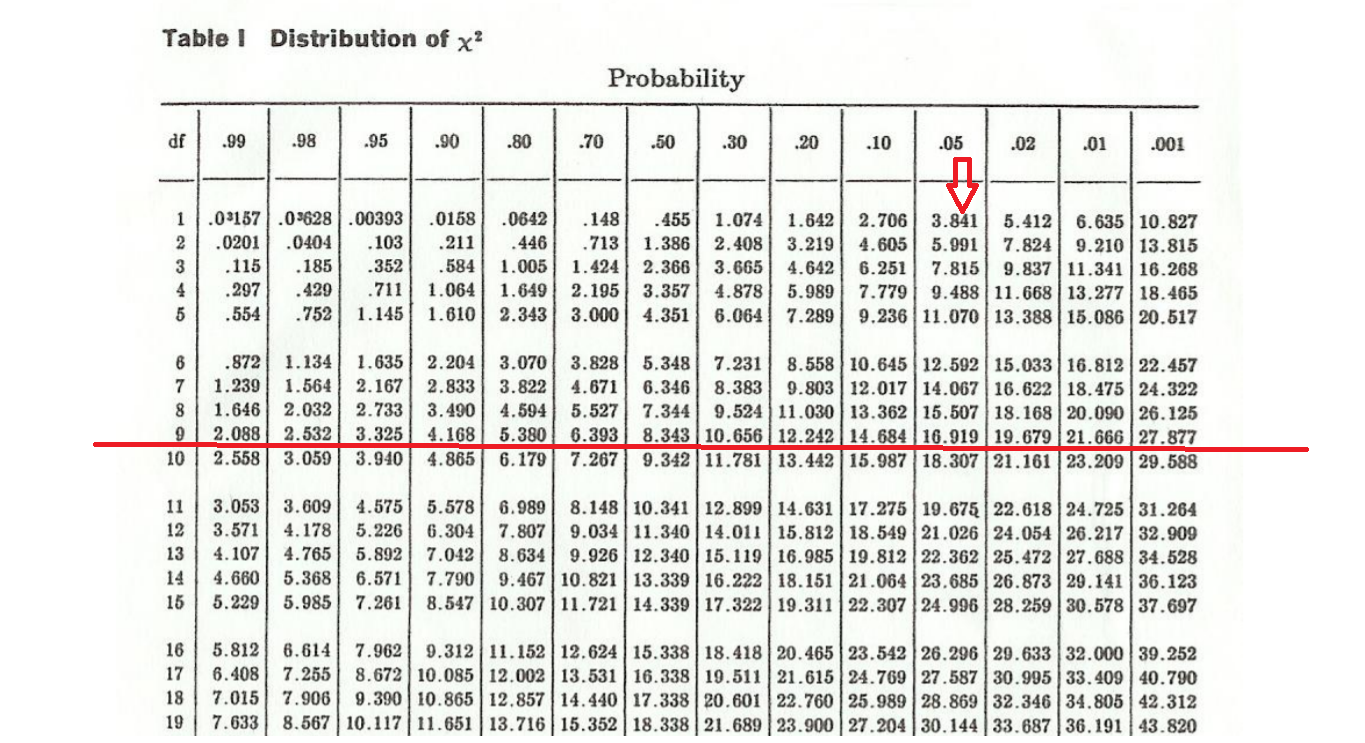
細かい数字が並んでいるだけでゲップがでそうになりますが(笑)・・・左端に「df」とあるのは教科書に「自由度」という言葉で解説されているものです。PLZは 0から 9まで 10ありますが、地名の合計値が決まっているので「自由に選べる数字は9」ということになります。何故なら9個決めると最後の10個目は合計から先に決めた9個の数字を引き算して一意的に決まってしまうからです。
まあ、面倒な話はさておき、ここは「自由度9」のライン上の数字を見てください。左の方は一桁の小さい数字が並んでおり、右に行くほど大きくはなりますが精々「20」くらいの数字です。この時、こういう数字が出現する確率は最上段の小数点の入った数字(確率)となります。
ごちゃごちゃ書きましたが、要は「635」なんて数字はこのテーブルから大きくはみ出したところにある=「-dorfとつく地名が、PLZに関係なく、すなわち地域性や歴史的な経緯に関係なく、全ドイツに均等に分布している」・・・なあんて、とてもじゃないけど言えたもんじゃないぜ!地域性や歴史的な経緯になんらか関係があるんだ!・・・ってことを表しているのです。
さて、改めて主要な地名siffixのリストを見てみましょう。その右端にあるカイ2乗にご注目ください。
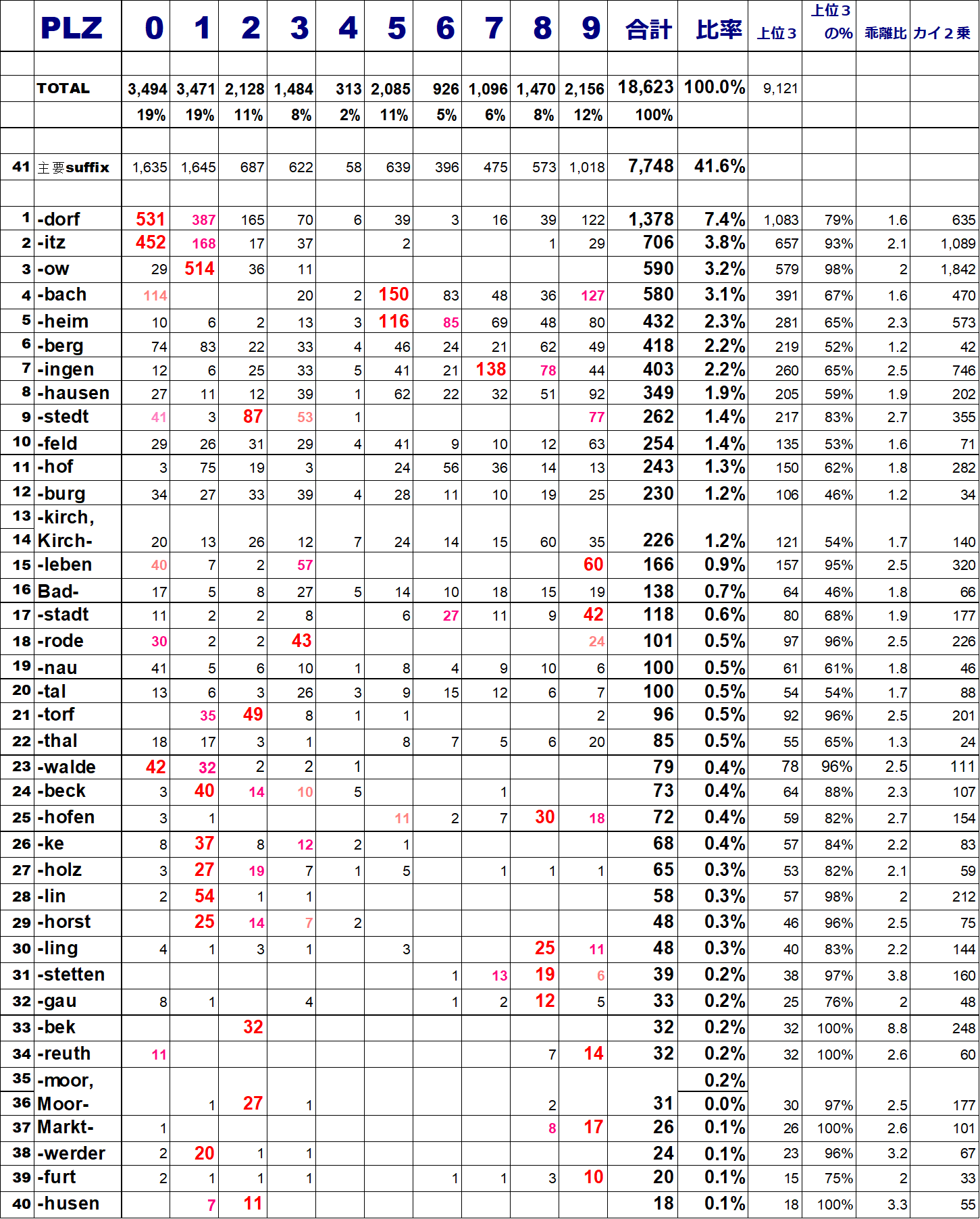
1,000を超える大きな数字もあり、全般に「地域性や歴史的な経緯に関係ない」とは言い切れないものが多いですが、中にいくつか二桁のものがあり、もう一息で全国均等に分布と言えそうなものもあります。
さて次回からは、この定量化したデータを使って、地名群をいくつかのタイプに分けてコメントしていきます。
地名の研究 Ortsnamenanalyse (6)に続きます





























